MODULE 6-9

GRATINGS

(4) Before you study this module, you should have studied elements and operation of a laser, coherence, propagation, interference, and diffraction. You also will find a knowledge of light helpful. Algebra and trigonometry are required to successfully complete this module.

1. Write a statement of definition or explanation for each of the following terms or concepts:

   Diffraction

   Constructive interference

   Destructive interference

   Transmission grating

   Reflection grating

   Replica grating

   Resolving power of a grating

   Blaze angle

   Efficiency

   Free spectral range

2. Differentiate between ruled gratings and holographic gratings by writing a short explanation of the manufacturing process for each.

3. Use the grating equation to calculate the wavelength of light incident on a grating.

4. Use experimental data to calculate the groove spacing and resolving power of a grating.

5. Choose from manufacturers’ data a grating designed to operate satisfactorily under given conditions.

6. Calculate the blaze angle of a reflection grating given the operating conditions.

DISCUSSION

(6) A highly periodic arrangement of finely spaced, parallel apertures is called a diffraction grating. The very first grating was used by a German physicist and astronomer, Joseph Von Fraunhofer. It consisted of a grid formed by winding fine wires on two parallel screw threads. This early diffraction grating looked similar to the one shown in Figure 1. The system had many obvious disadvantages.

Fig. 1
Early diffraction grating

(7) Present-day gratings consist of equidistant line rulings on a flat glass plate (transmission grating) or on a flat mirror (reflection grating). Depending on the application, the number of lines per millimeter typically ranges from less than one hundred to several thousand. Because of this extremely fine spacing, the lines are carefully scribed with a diamond tool in a special machine called a "ruling engine."

(8) Ruling a master grating is a very slow and highly controlled process. As you can imagine, producing a master grating is quite time consuming and costly. So the masters produced are used for making copies called "replicas." The replicas are made less expensively than the original by using a plastic or glass casting of the master grating.

(9) Today holographically recorded diffraction gratings are gaining wide acceptance. Holographically ruled diffraction gratings eliminate some of the problems encountered when the groove spacing is not perfect. They can be obtained with rulings as fine as 6000 lines per millimeter, which gives them high resolution. However, the efficiency of such gratings is typically lower than that of conventionally ruled gratings.

(10) You need an appreciation of diffraction theory to understand the operation of a diffraction grating. We won’t go into a thorough discussion of diffraction theory here, but a short review is appropriate at this time.

(11) The bending of a wave front as the wave passes through an opening or around an obstruction is a common example of diffraction. As an opening becomes much larger than the wavelength, diffraction effects become less noticeable. All periodic waves exhibit diffraction effects, but under certain conditions, such as broad spectral bandwidth, it may be hard to see the effects. Figure 2 shows diffraction taking place when plane waves pass through an aperture—such as a long narrow slit perpendicular to the page.

Fig. 2
Side view of plane wave diffraction through a long, narrow slit.

(12) When two such openings exist near each other, interference with other transmitted waves will result. This effect is shown in Figure 3 where monochromatic light waves are incident on two long, narrow, adjacent slits. The diffracted light through the slits may travel different distances before meeting at the screen. So the crests of one set of light waves may not necessarily coincide with the crests of the other.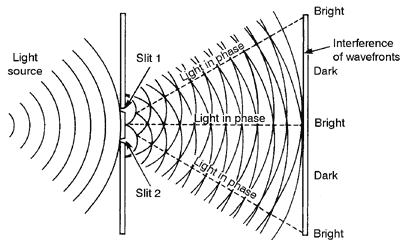

Fig. 3
Side view of interference of light diffracted by two long, narrow slits.

(13) Where crest and crest coincide on the screen, a region of brightness appears, and where a crest and trough coincide a region of darkness appears. The successive regions of brightness and darkness are called "interference fringes."

(14) A graph of the intensity of the light on the screen after interference is shown in Figure 4. Notice the uniformity of the pattern.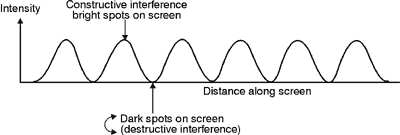

Fig. 4
Intensity of light produced by diffraction through two slits

(15) Figure 5 shows that light from S₁ and S₂ travels different distances to a given point P. The two rays arriving at P were in phase when they left slits S₁ and S₂ since both originated from the same wavefront in the incident plane wave.

Fig. 5
Different distances traveled by light from two slits

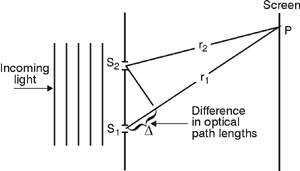
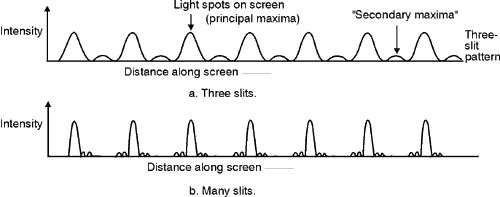
(16) Because the rays travel different optical path lengths in reaching P, they arrive at P with a phase difference. The number of wavelengths in the path length difference (r₁ – r₂ = D) determines the phase difference and therefore the nature of the interference at P.

(17) When there are three narrow, equally spaced slits, the interference pattern, instead of becoming more complicated, actually becomes more distinct. The additional slit imposes an extra condition on the three beams of light if they are all to interfere constructively at the same place. This has the effect of narrowing the bright region and at the same time making it brighter, since more light is concentrated there. Figure 6a shows a three-slit interference intensity pattern. Note the "secondary maxima" that appear between the "principal maxima." The number of secondary maxima increases as the number of slits increases, although, as shown in Figure 6b, the brightness of each secondary maximum decreases, until, with many slits, they disappear altogether, leaving only the principal maxima. When there are a large number of slits (thousands of them per centimeter) a diffraction grating is formed.

Fig. 6
Diffraction intensity patterns

(18) A clearer picture of the increased narrowing of the principal maxima with an increase in the number of slits is shown in Figure 7, for an increase from 5 slits to to 10 slits. For each case, seven orders of diffraction are shown, i.e., from m = 1 to m = 7. (The order of diffraction m is explained with Equation 1). As the order increases, the principal maxima are diffracted further and further from the spot locating the normal to the grating and is accounted for by the term "sin q_m," defined in Equation 1. Note that as the diffraction order increases, the intensity or brightness of each principal maximum decreases.

Fig. 7
Narrowing of principal maxima with increasing diffraction slits.

(19) Figure 8 shows a diagram of a transmission and reflection grating. The diffraction orders, to either side of the incident beam (m = –1, 0, +1, etc.) are also shown. The difference between the two gratings is that the transparent slits are considered to be individual "point sources" of light in the transmission grating while small reflecting surfaces are considered to be the individual "point sources" in a reflection grating.

(20) Transmission gratings seldom are used today. One reason for this is that light must pass through the glass or other material that forms the grating. So the light is subject to absorption and distortion caused by that material. Another reason is that reflection gratings yield more compact systems, because of the "folding" of the optical path through reflection.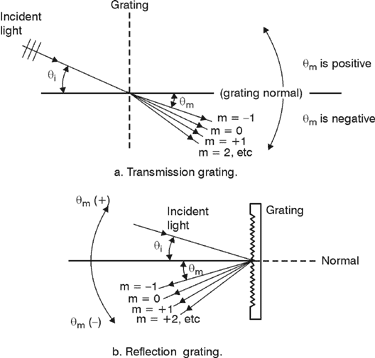

Fig. 8
Sign convention for grating equation (Equation 1) for
both a transmission (a) and a reflection (b) grating

(21) The position of a bright fringe on the screen is a function of the wavelength of light incident on the grating. As a result, different wavelengths—each a principal maximum—are focused at different locations on the screen. If the grating is illuminated by "white" light, the light is separated by the grating into its component wavelengths much as it is separated by a prism.

(22) The utility of a grating depends on the fact that there are unique sets of directions. For a given groove spacing and a given wavelength of light along these directions, the diffracted light from all the grooves is in phase.

(23) The grating equation that governs the location of the principal maxima as a result of diffraction is:

(24) Gratings are generally identified in terms of lines per inch or lines per millimeter. From this information, one can easily calculate the grating spacing a. For example, think of the lines that mark the "eighth" divisions on an inch ruler. There are 8 of them, starting just beyond the edge of a given inch mark. The spacing between the "eighth" lines are, as you know, one-eighth of an inch. You get this by dividing the inch length by 8 lines, getting 1/8 inch/line, or just 0.125 inch. It's the same way with a grating. If the grating has 8,000 lines per inch, then the grating-spacing is:

(25) If the grating has 2000 lines per millimeter, then the grating spacing is

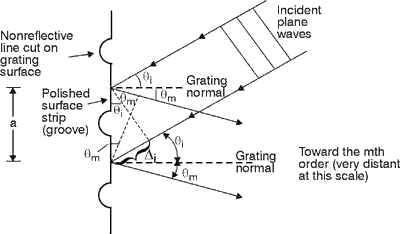
(26) You can visualize the meaning of the symbols in Equation 1 better from the geometry of Figure 9. Here a plane wavefront is incident on a grating surface at an angle q_i measured with respect to the grating normal. Then, via reflection, it’s diffracted at an angle q_m measured with respect to the same normal. The groove spacing is designated by a. Notice that q_i and q_m are not necessarily equal due to the fact that light diffracts in all directions from the thin strips of polished surface between the grooved lines.

Fig. 9
Cross section of a small segment of a reflection grating surface

(27) You can see by Equation 1 that, for a given order m and grating spacing a, there is a mathematical relationship between the wavelength of the incident light and the angles of the incident and diffracted rays. See in Figure 9 that the geometrical path difference between light diffracted from successive grooves is simply D = D_i – D_m = (a sin q_i – a sin q_m). The principle of interference dictates that only when the angles q_i and q_m are such that this difference equals the wavelength of the light, or an integral multiple ml thereof, will the light from all grooves interfere constructively. At all other angles, there will be some degree of destructive interference between the light rays of this wavelength coming from the grating.

(28) So when light of wavelength l hits a grating at a given incident angle, there’s a unique set of diffraction angles at which the light will leave the grating, reinforced one for each different order. At all other angles its intensity will be reduced. This property lets us use gratings in instruments to measure wavelengths of light and to study the structure and intensity of spectral lines. Such instruments include spectroscopes, spectrophotometers, monochromators, spectrographs and spectrometers.

(29) Further interpretation of Equation 1 shows that, for certain sets of angles q_i and q_m and groove spacing a, the grating diffracts the light into different orders (m = 1, 2, 3, etc.). To be reinforced, the light coming from successive grooves must differ in phase by a whole number of wavelengths. This happens first when the difference is one wavelength, in which case we speak of first-order (m = 1) diffraction. It happens again when the difference is two wavelengths (m = 2), called the second order, and so on. The angle q_m increases as the order increases.

(30) The most troublesome aspect of the multiple-order behavior of gratings is that successive orders can overlap. For example, the violet wavelength 400 nm of the second order (m = 2) will reinforce at the same position on the screen as the deep red wavelength 800 nm of the first order.

(31) We can overcome the overlapping of multiple orders by suitable filtering or by detector selectivity. More overlapping of wavelength regions occurs in the higher spectral orders than in the lower orders.

Efficiency

(32) Two forms of efficiency are considered in connection with diffraction gratings. The absolute efficiency is the ratio of power diffracted at a particular wavelength (l) in the order of interest to the power incident on the grating at that wavelength (l). The relative efficiency takes into account the reflectivity of the grating’s metallic surface and is the ratio of the energy diffracted by the grating at a particular wavelength (l) in the order of interest to the energy reflected by a mirror under the same working conditions. A relationship exists between the two efficiencies such that:

Absolute efficiency = Relative efficiency × reflectance of the mirror.

(33) The mirror mentioned in the formula must have the same coating as the grating. And it must work in the same angular conditions as the grating. The efficiency of a grating is generally greatest at the blaze wavelength (see discussion on blaze which follows) in ruled gratings or at a particular wavelength of interest for holographic gratings. Figure 10 shows an efficiency curve for both ruled gratings and holographic gratings.

Fig. 10
Efficiency curve of a holographic grating is generally lower
but flatter than that of a ruled grating.

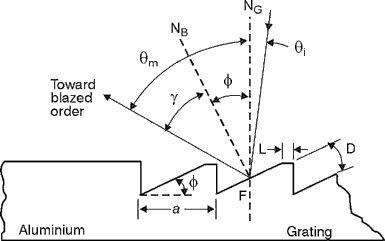
Blaze

(34) It’s possible with a reflection grating to concentrate most of the diffracted spectral energy into one spectral order and reduce the energy in all other orders. This redistribution of energy among the orders depends on the angle between the reflecting element and grating surface. This angle is called the "blaze angle" f. See Figure 11. Note that the light reflects preferentially toward the "blazed order." In other words g » f + q_i, where N_G = grating normal, N_B = blaze normal.

Fig. 11
Blazed groove profile

(35) The diffraction spectral intensity curve shown in Figure 6 can be changed to that shown in Figure 12b when the grating is blazed for the first order.

(36) Figure 12 shows how all orders are virtually extinguished and the available energy is concentrated mostly into a single order. This phenomenon occurs for only one wavelength, which is called the "blaze wavelength." Under these conditions, the specular reflection from the grating surface and the mth order diffraction occur at the same, or nearly the same, angle. This causes most of the diffracted light to go into the blazed order (Figure 12b). You can find the relationship between the blaze angle and blaze wavelength by applying the grating formula (Equation 1). When you apply the equation, you find that a grating blazed for a given wavelength in the first order also is blazed for half that wavelength in the second order and one-third of the wavelength in the third order, and so on.

 Fig. 12
Diffraction pattern for an unblazed grating (top) and for a grating blazed
in first order (bottom)

(37) When speaking of a grating blazed at a given wavelength, it is implied that the grating is blazed in a certain specified order for this wavelength and for Littrow use (light incident normal to the reflecting elements).

(38) A grating blazed for use in low orders (1 or 2) is called an "echellette." A grating blazed for use in higher orders ( > 10) is called an "echelle" grating.

Resolving Power

(39) The resolution or chromatic resolving power of a grating describes its ability to separate adjacent spectral lines. Resolution generally is defined as , where Dl is the difference in wavelength between two equal intensity spectrum lines that are just separated.

(40) The limit of resolution of a grating is theoretically R = mN, where m is the grating order and N is the total number of grooves illuminated on the grating. To increase the resolution we could think of increasing N by obtaining a finer-ruled grating. However, you must know that, if you do this, certain orders disappear and the maximum value for m decreases. You get a more useful expression for resolution by substituting for m from the grating equation and arriving at Equation 2.

Equation 2

(41) Since (sin q_i + sin q_m) can have a maximum value of 2, the maximum resolving power at any wavelength turns out to be equal to 2 Na/l, where N is the number of slits and a is the slit spacing. So the product Na is the illuminated width w of the grating. At 500 nm a 15-cm grating will have a maximum resolution of:

Types and Uses of Gratings

(42) Gratings can be either plane or concave. Plane gratings are usually less expensive and easier to control in the manufacturing process. Concave gratings, however, offer the added advantage of focusing. This eliminates one element such as a lens from the optical system.

(43) Groove spacing is a wide open variable in gratings. For useful diffraction, the spacing must be at least 2/3 of the longest wavelength of interest. But in some cases it can be as much as 100 wavelengths or more. Rulings as fine as 3600 lines per millimeter can be made. This is a spacing of about half the wavelength of visible light.

(44) One of the most widely used applications of the diffraction grating is in spectroscopy. The spectroscope is used to study the optical spectra of incandescent sources to determine their composition, temperature, or motion—as in stars moving toward us or away from us.

(45) Figure 13 shows a simple grating spectroscope that’s used for analyzing the spectrum of a light source assumed to emit a number of discrete wavelengths or "spectral lines." The light from source S is focused by lens L₁ onto slit S₁ placed in the focal plane of lens L₂. The collimated light emerging from collimator C falls on the grating G. Rays of light associated with a particular interference maximum occurring at angle q form a parallel beam that enters the camera or field lens L₃. The image of the slit thus is focused onto plane F–F ' and is examined with the magnifying eyepiece E.

Fig. 13
A simple transmission grating spectroscope used to analyze wavelengths
of light emitted by source S

(46) A typical pattern that you might see with a spectroscope is shown in Figure 14. The lines actually appear as different colors, and their spacings and individual color tell much about the properties of the source.

Fig. 14
Typical spectrograph pattern

(47) Instruments much like that of Figure 13 are used to learn many facts about the age and composition of planets and stars. The light falling on a telescope lens from the stars may be sent through a grating. Then the spectrum formed by the starlight is studied to tell important facts about bodies billions of miles away.

(48) Two special ways of using a grating as a spectrograph are important enough to deserve mention. The first is the autocollimating or "Littrow" scheme. As shown in Figure 15a, the slit source is at the focus of a collimating lens positioned close to the grating G. The grating is rotated on an axis parallel to the grooves to select the diffraction wavelength. The chosen light returns through the lens and is refocused near the original slit. This type of spectrograph is generally more compact than the others.

Fig. 15
"Littrow" scheme

(49) Compare the geometry in Figure 15b of the Littrow configuration for a blazed reflection grating to Figure 11. Note that the incident and diffracted rays are nearly parallel to the blaze normal N_B such that a » b » 0 and q_i » f, q_m » –f. Note also that f – q_i = –q_m – f (q_m is negative by sign convention). Therefore f = 1/2 (q_i – q_m). In this configuration the grating equation reduces to ml = 2a sin f.

(50) The spectrometer shown in Figure 16 uses two mirrors to control the light as the grating is rotated for a spectral scan.

Fig. 16
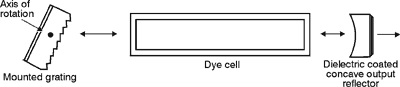
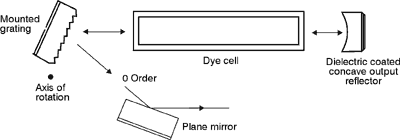
Double-slit spectrometer

(51) Field stops and stray light baffles must be used to prevent reflection from one slit to another and to control scattered light within the system. These types of instruments are sometimes used as monochromators to select or filter out one single wavelength of light from many wavelengths present.

(52) Another important use of the diffraction grating is in wavelength tuning and selectivity in laser cavities. There are two ways of using a grating as part of a laser cavity. A plane diffraction grating can be used as the "total" reflector (Figure 17) or as the "output" reflector (Figure 18) in a laser cavity, or as an intermediate reflector to "fold" the cavity (not shown).

Fig. 17
Littrow configuration grating as total reflector

Fig. 18
Grating as output reflector

(53) You can tune the output wavelength of the dye laser by turning the diffraction grating end reflector about an axis parallel to the grooves. Using a grating as one of the reflectors in a dye laser causes the spectral line width of the output to be reduced to a narrow region around the diffracted wavelength.

Care and Cleaning of Gratings

(54) Good reflectivity is achieved in modern gratings by applying an evaporated aluminum or other metallic coating to the replica of the master grating. The aluminum coating is rather soft, as well as very thin, and is placed on a plastic replica. Both are easily damaged.

(55) Foreign matter such as dust and fingerprints seriously alters the grating’s performance. Fingerprints and oral spray are ever-present hazards. Gratings should be given maximum protection from contamination, and the utmost care in necessary handling. Safe cleaning techniques are very limited and should be attempted by experts.

(56) Table 1 is a composite summary of the properties of gratings that you must consider when you select a grating.

Table 1. Properties of Diffraction Gratings

1. Define or explain the following terms or concepts:
   Diffraction
   Constructive interference
   Destructive interference
   Transmission grating
   Reflection grating
   Replica grating
   Resolving power of a grating
   Blaze angle
   Efficiency
   Free spectral range

2. In your own words briefly explain the manufacturing process used for ruled gratings and for holographic gratings.

3. Calculate the wavelength of light incident normally upon a grating with 14,300 lines per inch when a second-order image is produced at a 33° angle.

4. Calculate the groove spacing and the maximum resolving power of a reflection grating that has a width of 5 centimeters. The grating will diffract light of 546 mm to a first-order image at an angle of 15° when the light is incident along the normal to the grating surface.

5. A tunable dye laser is to operate in a frequency range of 400 nm to 800 nm. A reflection grating is to be used as a tunable end reflector. The grating must be one inch in diameter and be approximately one-half inch thick. It should be blazed to operate in the first order at a wavelength of 600 nm. There should be approximately 15,000 lines per inch on the grating. Use catalogs from three manufacturers to compare gratings with the given specifications. Choose a grating from one of the manufacturers to recommend for purchase. Give the reasons why you recommended this grating.

6. A blazed reflection grating will be used as the HR in a dye laser (l = 560 nm). The grating will have 1000 lines/mm and is to be used in 3rd order. What is the blaze angle f? (Hint: See Figure 15b.)

7. Consider the same dye laser and Littrow grating as in Exercise 6. Approximately what angle should the grating be rotated through to tune the laser from 560 nm to 590 nm? Which way should the grating be rotated? Draw a sketch.

HeNe laser

Transmission grating

Reflection grating

Screen

Optical bench and mounts for gratings

Mercury arc or helium arc lamp

Measurement of Grating Spacing and Resolving Power

1. Arrange a HeNe laser so that the beam is incident normally on a transmission grating as shown in Figure 19. With this arrangement, the grating equation (Equation 1) reduces to ml = a sin q_m.
   

    Fig. 19
   Experimental arrangement

2. Using trigonometry, determine q_m by measuring L and d as shown on Figure 19. Do this for at least the first three orders. Record your results in a data table you prepare for that purpose.

3. Calculate the groove spacing a using the reduced grating equation. Average the results obtained for each order used.

4. Repeat the above procedures using a reflection grating instead of the transmission grating. Make appropriate changes in the experimental arrangement.

5. Assuming that the entire grating surface is illuminated, calculate the resolving power for each grating using Equation 2. Assume the incident light to be from a HeNe laser.

Determination of Wavelength of a Light Source

1. Arrange either of the gratings used in the first experiment so that light from a light source other than the HeNe laser can be incident upon the grating and then transmitted or reflected to a screen. Light sources such as a mercury arc, sodium arc or sodium flame will suffice.

2. Using the average value for the groove spacing as determined in the first experiment, make the measurements necessary to calculate the wavelength of one spectral line in the incident light.

3. Compare your value for the wavelength of this light with accepted values given in charts or handbooks.

4. Compute the percent error of your measurements.

"Handbook of Diffraction Gratings—Ruled and Holographic." Metuchen, NJ: Prepared by the staff of JoBin-Yvon, Inc.

Jenkins, F., and H. White. Fundamentals of Optics, 4th edition. New York: McGraw-Hill, 1976.

Kingslake, Rudolph, ed., Applied Optics and Optical Engineering, Vol. V., New York: Academic Press, 1969.

Pedrotti, Frank L., and Leno S. Pedrotti. Introduction to Optics, Chapter 20. Englewood Cliffs, NJ: Prentice-Hall, 1987.